行列も実数と同じように2乗(自乗)することができます。
行列の2乗
行列に自分と同じ行列を掛ければそれが行列の2乗です。
ただし、2乗できる行列には条件があります。
行列が2乗できるのは、その行列が正方行列である場合に限ります。
なぜなのかは、すぐにわかります。正方行列でないと自分自身をかけることができないからですね。
2乗が計算できない行列の例
\[A=\begin{pmatrix}1 & 3 & 5 \\ 2 & 4 & 6\end{pmatrix}\]
この行列は、2行3列の行列で正方行列ではありません。
したがって、その行列の2乗は、積が定義されていないため、計算できません。
\[ A^2=AA=\begin{pmatrix}1 & 3 & 5 \\ 2 & 4 & 6\end{pmatrix} \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6\end{pmatrix} \]
この式は、行列の積ができる形に該当しないので計算できないのです。
ちなみに、
\[\begin{pmatrix}1 & 3 & 5 \\ 2 & 4 & 6\end{pmatrix} \begin{pmatrix}1 & 2 \\ 3 & 4 \\ 5&6 \end{pmatrix}\]
だったら計算できますが、これは2乗とは言いません。
かける順番を変えて
\[\begin{pmatrix}1 & 2 \\ 3 & 4 \\ 5&6 \end{pmatrix} \begin{pmatrix}1 & 3 & 5 \\ 2 & 4 & 6\end{pmatrix}\]
も計算可能ですが、これも二乗と言いません。
二乗が計算できる行列は正方行列の場合に限ります。
行列の2乗の計算例
正方行列なら2乗は計算可能です。
行列の2乗は普通の数のように簡単には計算できません。行列の掛け算が普通の数とちょっと違っているからです。
行列の掛け算をするときに、(心のなかで)「ぎょうれつ、ぎょうれつ、ぎょうれつ」と唱えながら計算していくことからわかるように、行列の掛け算は、「行」と「列」の組み合わせで掛け算します。
2次の正方行列(2×2行列)の2乗
簡単な2次の正方行列の例で2乗を計算してみます。
\(B=\begin{pmatrix}1&2\\3&4\end{pmatrix}\)
の2乗は、\(B^2\)と書きます。計算すると、
\(B^2=B\cdot B\\= \begin{pmatrix}1&2\\3&4\end{pmatrix} \begin{pmatrix}1&2\\3&4\end{pmatrix}\)
\(= \begin{pmatrix}1*1+2*3&1*2+2*4\\3*1+4*3&3*2+4*4\end{pmatrix} \)
\(= \begin{pmatrix}7&10\\15&22\end{pmatrix} \)
となります。
念のため、\(B^2\)は、各成分を2乗した\( \begin{pmatrix}1&4\\9&16\end{pmatrix}\)とはなりません。
暗算ではちょっと難しいですね。
3次の正方行列(3×3行列)の2乗
3次の正方行列の例です。
\[C=\begin{pmatrix}1 & 2 & 3 \\ 2 & 2 & 2 \\ 1&1&1\end{pmatrix}\]の二乗を計算してみます。
\[C^2 =\begin{pmatrix}1 & 2 & 3 \\ 2 & 2 & 2 \\ 1&1&1 \end{pmatrix} \begin{pmatrix}1 & 2 & 3 \\ 2 & 2 & 2 \\ 1&1&1\end{pmatrix} \]を計算すればよいのですが、まず、1行目の成分(1, 2, 3 )と1列目の縦成分(1, 2, 1)をそれぞれ掛けて足し合わせます。\(1*1+2*2+3*1=8\)これが答えの1行1列の成分です。
次に1行目の成分(1, 2, 3)と2列目の成分(2, 2, 1)をそれぞれ掛けて足し合わせます。\(1*2+2*2+3*1=9\)これが答えの1行2列の成分です。
ここまでの計算途中を書くと
\(C^2=\begin{pmatrix}8 & 9 & \, \\ \, & \, & \, \\ \,& \, & \,\end{pmatrix}\)となっています。
同様にしてすべての成分を計算すると、
\(C^2=\begin{pmatrix}8 & 9 & 10 \\ \, 8 & 10 & 12 \\ 4 & 5 & 6\end{pmatrix}\)となります。
対角行列の2乗の計算例
実は、対角行列に関しては2乗の計算が楽になります。
どうしてかというと、それぞれの成分をそのまま2乗すればよいからです。
3次の正方行列を例として、公式として書くと
\[\begin{pmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & c \end{pmatrix}^2= \begin{pmatrix}a^2 & 0 & 0 \\ 0 & b^2 & 0 \\ 0 & 0 & c^2 \end{pmatrix}\]
となります。
参考サイト
下記のサイトで行列の2乗が計算できます。

参考サイトの使い方(計算方法)
下記のような画面が表示され、操作すると行列の2乗の計算ができます。
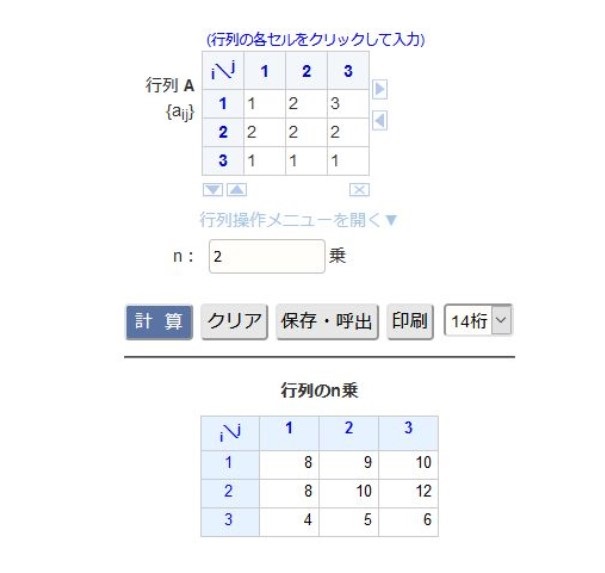
画面の説明です。
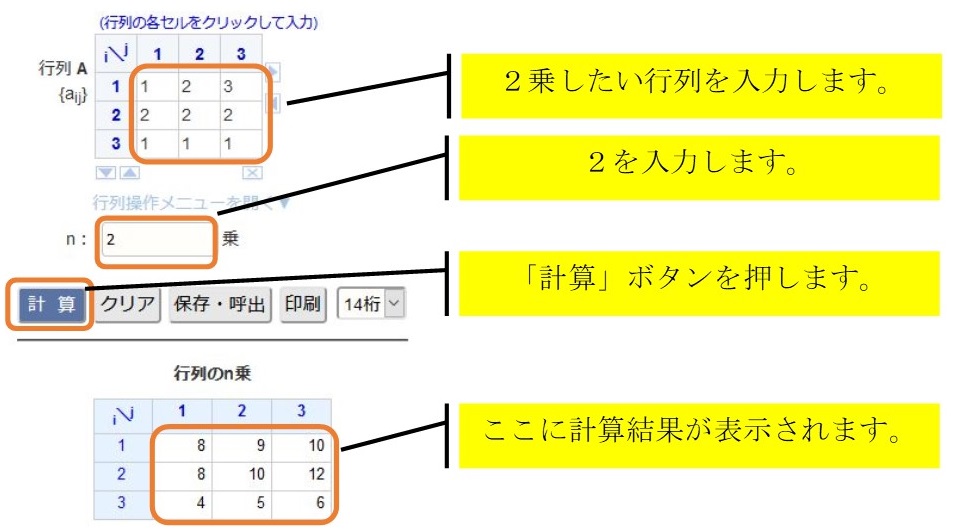
この例は、3x3行列の2乗を計算した例ですが、4x4行列や3乗、4乗の計算もできます。

